Srpska sarma ili repetitorijum iz statistike

Pitanje prosečne plate, kao reprezenta standarda građana, stalno se provlači kroz medije i izvor je brojnih polemika i skepse prema statistici kao nauci. Ovaj članak ima za cilj da bar delimično razjasni najvažnije nedoumice i pokaže da statistika poseduje instrumente reprezentovanja podataka na način koji bi sačuvao i preneo relevantne informacije, ali je ovo moguće samo ako se to ne čini tendenciozno.

Kod većine ljudi postoji izražena tendencija da pod terminom "prosečno" podrazumevaju aritmetičku sredinu, pa tako prosečna primanja zaposlenih izračunavaju sabravši sve pojedinačne iznose i onda taj broj podele sa brojem zaposlenih. Nije iznenađujuće, međutim, što ovakav pristup dovodi do besmislenih zaključaka, poput onog čuvenog: jedan čovek jede meso, drugi jede pirinač a treći – kupus, pa odatle, u proseku, jedu sarmu. Statističari su ovaj problem odavno uočili i matematička statistika danas poseduje nebrojene alate za obradu i iskazivanje rezultata. Ovo, međutim, kod mnogih proizvodi utisak da je statistika, kao nauka, podložna nekoj vrsti prostitucije, pošto se može zloupotrebiti da se izvuku najrazličitiji (i često, međusobno nespojivi) zaključci. Istina je, međutim, nešto drugačija. U statistici, kao i u novinarstvu koje teži da se bavi njenom interpretacijom, važi poznato pravilo da "papir trpi sve", odnosno, statistika je samo onoliko tačna koliko je ispravno primenjena i koliko su tačni podaci kojima barata.

U nedavno objavljenom članku u NSPM "Kruženje standarda u prirodi" [1] autor se pozabavio kritikom drugog članka objavljenog u listu "Danas" [2]. Izvorni članak iz "Danas"-a bavi se interpretacijom statističkih pokazatelja na osnovu kojih, navodno, izlazi da se danas u Srbiji živi mnogo bolje nego ranije. Autor kritičkog članka opravdano primećuje da je besmisleno "potezati prosečnu platu od 35.000 dinara" kada je potrebno opisati situaciju u kojoj npr. 28 zaposlenih prima po 15.120 dinara, dok jedan zaposleni, direktor, prima 600.000. Intuitivno je jasno da je učinjena greška, iako kada se izračuna, izlazi da je prosek blizu deklarisanih 35.000 dinara. Gde je problem?

Ovakva logika bi bila ispravna u situaciji u kojoj bi postojala "uravnilovka" odnosno kada bi primanja bila manje-više jednaka i simetrično raspoređena oko tog "proseka". Kada je, međutim, raspodela primanja u populaciji izraženo asimetrična, pojam "prosečna plata", izračunat kao obična aritmetička sredina (sabrati sve plate i podeliti sa brojem zaposlenih) očigledno gubi smisao. Zato u statistici postoje razni drugi načini da se prikažu podaci, a kao mere tog "proseka", pored aritmetičke sredine, postoje još i "medijana" i "mod". Na samom početku svakog ozbiljnog kursa iz statistike, ovi pojmovi se jasno definišu i razgraničavaju. Tako, npr. u čuvenoj knjizi "Prvi Kurs Matematičke Statistike" [3], već na prvoj strani razmatra se aritmetička sredina, a već na trećoj – medijana i tzv. percentili. Čitaocu ove knjige nije teško da shvati šta je medijana: u slučaju plata, to je ona vrednost od koje polovina zaposlenih ima manju, a druga polovina veću platu. Drugim rečima, ako se kao "prosečna plata" saopšti medijana, onda je to onaj iznos koji razgraničava dve polovine zaposlenih: one koji imaju manje od onih koji imaju više od tog iznosa. Kako bi ovo bilo jasnije, zamislimo hipotetičko preduzeće sa 33 zaposlena i sledećim neto prihodima (Tabela 1):

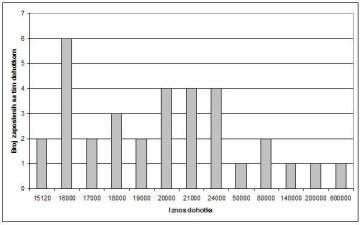
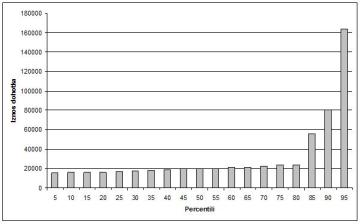
Aritmetička sredina, koju obično nazivamo prosečnom platom, bila bi približno 50.371 dinar. Međutim, medijana bi bila 20.000 dinara. Dakle, 50 % zaposlenih u ovom preduzeću ima prihode ispod 20.000 dinara (logično, ostalih 50 % prima više od toga). Odavde se vidi da je neophodno jasno definisati šta tačno znači "prosečna plata". Medijana je statistička mera koja, u ovom slučaju, bolje pokazuje kako zaposleni, u proseku, stoje sa primanjima.

Međutim, ovde se ne treba zaustaviti. Da bi se ostvario potpuniji uvid u raspodelu dohotka po zaposlenima, koriste se različiti dijagrami. Ovo je naročito važno kada se radi sa velikim populacijama (statistike koje se odnose na celo stanovništvo), a ovde ćemo iskoristiti primer iz Tabele 1 radi ilustracije. Grafikon 1 prikazuje raspodelu dohotka po zaposlenima. Sa njega se vidi, na primer, da 6 zaposlenih ima primanja u iznosu 16.000 neto, zatim 2 zaposlena imaju primanja 80.000 i sl. Bez informacija koje su dostupne sa ovakvih dijagrama, tvrdnje da se "u proseku živi bolje" svode se na priču o sarmi sa početka ovog teksta, jer se ne zna koliko zaposlenih zapravo imaju kolika primanja.

U realnim situacijama, vrednosti iznosa dohotka bi bile prikazane kao opsezi (npr. "od 16.000 do 18.000 dinara" i sl.) čime bi se formirali tzv. rangovi. Na osnovu ovakvog dijagrama, datog za celo stanovništvo, saznali bismo koliko ima ljudi sa primanjima "od 16.000 do 18.000" a koliko npr. "od 160.000 do 500.000".

Koristan dijagram bi bio i onaj koji prikazuje raspodelu dohodaka po tzv. percentilima (termin objašnjen takođe na samom početku kursa, na str. 3 knjige ). Šta bi bio npr. 90-ti percentil? To bi bio onaj iznos plate ispod koga se nalazi 90 % svih plata zaposlenih. Pogledajmo Grafikon 2: vidi se da npr. 90-tom percentilu odgovara iznos dohotka od 80.000 dinara, što znači da, u primeru preduzeća iz Tabele 1, devedeset odsto zaposlenih prima manje od 80.000 dinara. Osamdeseti percentil iznosi 24.000 dinara, dakle 80 % zaposlenih prima manje od toga. Objavivši ovakav dijagram, novinar obezbeđuje tačniju interpretaciju stanja u preduzeću ili celokupnoj ekonomiji, odnosno više nije moguće nekome "prodati" priču o sarmi. Takođe je očigledno da nije reč o nekoj složenoj i teško shvatljivoj matematici, koja se ne može objasniti čitaocima, kao i da nije tačno da statistika ne poseduje instrumente reprezentovanja podataka na način koji bi sačuvao i preneo relevantne informacije.

Nakon ove male "analize", pozabavimo se i pojedinostima iz izvornog članka. Za primer uzmimo tvrdnju "danas je za potrošačku korpu potrebno izdvojiti malo više od jedne plate, što znači da u većini kuća u Srbiji ipak preostane i nešto novca za ostale potrebe". Izlazi da, iako je plata manja od "potrošačke korpe", ipak "preostane i za ostale potrebe" (?) Ovaj nelogični zaključak možda proističe iz pretpostavke da "prosečna porodica" ima više od jednog zaposlenog člana; mada se zanemaruje veliki broj nezaposlenih, pozabavimo se manje očiglednim problemom. Koliko je to "većina kuća"? Na primeru našeg preduzeća, izlazi da je "prosečna plata", izračunata kao obična aritmetička sredina od 50.371 dinar, više nego dovoljna za podmirenje "potrošačke korpe" (autor navodi da je oko 35.000 dinara skoro dovoljno). Sa Grafikona 2, međutim, vidi se da, u tom preduzeću, 80 % zaposlenih prima manje od 24.000 dinara (kako je već objašnjeno) pa postaje jasno da ovakav zaključak, iz podatka o "prosečnoj plati", nije moguće izvesti. Naprotiv, primer pokazuje da je statistika, potpomognuta odgovarajućim instrumentima grafičkog prikazivanja, sasvim sposobna da pokaže da li je zaista "u većini kuća u Srbiji" dovoljno novca. U preduzeću iz navedenog primera, 80 % čini većinu, a oni nemaju dovoljna primanja da podmire "potrošačku korpu" i pored "prosečne plate" od 50.371 dinara.

Ovo je samo jedan primer pogrešnog zaključivanja u statistici. Kakva god da je metodologija koja se pominje, krupno je pitanje i kakva se korekcija unosi pri obračunu prihoda nezaposlenih lica. Ova korekcija je, naime, neophodna, pošto i ljudi bez primanja (uključujući i zaposlene kojima kasni plata) moraju podmirivati bar osnovne troškove kao i zaposleni. Njihova primanja se mogu obračunati kao nula, a moguće je i uvesti realističniju korekciju: npr. u porodici čiji je jedan član nezaposlen a drugi ima primanja od npr. 20.000 dinara, računati kao da oboje imaju primanja od 10.000 dinara. Neobično je teško, međutim, u medijima naći makar i osnovni opis kakva se korekcija ovde pravi. Postoji i serija drugih problema na koje su ukazali brojni čitaoci-komentatori na sajtovima gde se pojavio članak u celini ili u delovima. Poređenje dinara u odnosu na evro, bez uzimanja u obzir inflacije i gubitka vrednosti samog evra je jedan od njih: koliko se robe ili usluga moglo platiti sa 100 evra pre 10 godina a koliko može danas, ili koliko se moglo kupiti za "ekvivalent" od približno 200 nemačkih maraka pre 20 godina? Pominjanje frižidera kao repera cena: frižider, kao i nameštaj, retko se nabavlja, dok se hrana, komunalije, gorivo, električna energija i sl. moraju redovno i neizbežno plaćati, a koliko se njihova cena promenila u poslednjih deset godina?

Iako možda na prvi pogled to nije očigledno, cilj ovog teksta nije direktna kritika na račun zaključaka iz članka objavljenog u "Danas"-u. Autor ovog teksta ne sumnja u stručnost naših statističara, ali smatra da se njihovi rezultati neadekvatno reprezentuju putem medija. Namera autora nije ni da dovodi u pitanje ili kritikuje Paretovo pravilo [4] već da podigne nivo svesti čitalaca o tome šta je zaista statistika i kako se ona često nepravilno koristi u cilju tumačenja podataka vezanih za standard građana.