| Економска политика | |||
Српска сарма или репетиторијум из статистике |
 |
 |
 |
| недеља, 06. јун 2010. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Код већине људи постоји изражена тенденција да под термином "просечно" подразумевају аритметичку средину, па тако просечна примања запослених израчунавају сабравши све појединачне износе и онда тај број поделе са бројем запослених. Није изненађујуће, међутим, што овакав приступ доводи до бесмислених закључака, попут оног чувеног: један човек једе месо, други једе пиринач а трећи – купус, па одатле, у просеку, једу сарму. Статистичари су овај проблем одавно уочили и математичка статистика данас поседује небројене алате за обраду и исказивање резултата. Ово, међутим, код многих производи утисак да је статистика, као наука, подложна некој врсти проституције, пошто се може злоупотребити да се извуку најразличитији (и често, међусобно неспојиви) закључци. Истина је, међутим, нешто другачија. У статистици, као и у новинарству које тежи да се бави њеном интерпретацијом, важи познато правило да "папир трпи све", односно, статистика је само онолико тачна колико је исправно примењена и колико су тачни подаци којима барата. У недавно објављеном чланку у НСПМ "Кружење стандарда у природи" [1] аутор се позабавио критиком другог чланка објављеног у листу "Данас" [2]. Изворни чланак из "Данас"-а бави се интерпретацијом статистичких показатеља на основу којих, наводно, излази да се данас у Србији живи много боље него раније. Аутор критичког чланка оправдано примећује да је бесмислено "потезати просечну плату од 35.000 динара" када је потребно описати ситуацију у којој нпр. 28 запослених прима по 15.120 динара, док један запослени, директор, прима 600.000. Интуитивно је јасно да је учињена грешка, иако када се израчуна, излази да је просек близу декларисаних 35.000 динара. Где је проблем? Оваква логика би била исправна у ситуацији у којој би постојала "уравниловка" односно када би примања била мање-више једнака и симетрично распоређена око тог "просека". Када је, међутим, расподела примања у популацији изражено асиметрична, појам "просечна плата", израчунат као обична аритметичка средина (сабрати све плате и поделити са бројем запослених) очигледно губи смисао. Зато у статистици постоје разни други начини да се прикажу подаци, а као мере тог "просека", поред аритметичке средине, постоје још и "медијана" и "мод". На самом почетку сваког озбиљног курса из статистике, ови појмови се јасно дефинишу и разграничавају. Тако, нпр. у чувеној књизи "Први Курс Математичке Статистике" [3], већ на првој страни разматра се аритметичка средина, а већ на трећој – медијана и тзв. перцентили. Читаоцу ове књиге није тешко да схвати шта је медијана: у случају плата, то је она вредност од које половина запослених има мању, а друга половина већу плату. Другим речима, ако се као "просечна плата" саопшти медијана, онда је то онај износ који разграничава две половине запослених: оне који имају мање од оних који имају више од тог износа. Како би ово било јасније, замислимо хипотетичко предузеће са 33 запослена и следећим нето приходима (Табела 1):
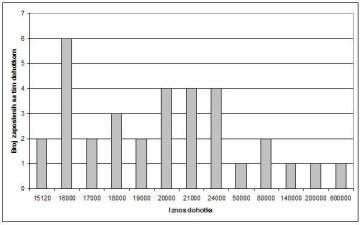
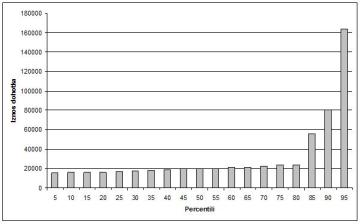
Аритметичка средина, коју обично називамо просечном платом, била би приближно 50.371 динар. Међутим, медијана би била 20.000 динара. Дакле, 50 % запослених у овом предузећу има приходе испод 20.000 динара (логично, осталих 50 % прима више од тога). Одавде се види да је неопходно јасно дефинисати шта тачно значи "просечна плата". Медијана је статистичка мера која, у овом случају, боље показује како запослени, у просеку, стоје са примањима. Међутим, овде се не треба зауставити. Да би се остварио потпунији увид у расподелу дохотка по запосленима, користе се различити дијаграми. Ово је нарочито важно када се ради са великим популацијама (статистике које се односе на цело становништво), а овде ћемо искористити пример из Табеле 1 ради илустрације. Графикон 1 приказује расподелу дохотка по запосленима. Са њега се види, на пример, да 6 запослених има примања у износу 16.000 нето, затим 2 запослена имају примања 80.000 и сл. Без информација које су доступне са оваквих дијаграма, тврдње да се "у просеку живи боље" своде се на причу о сарми са почетка овог текста, јер се не зна колико запослених заправо имају колика примања. У реалним ситуацијама, вредности износа дохотка би биле приказане као опсези (нпр. "од 16.000 до 18.000 динара" и сл.) чиме би се формирали тзв. рангови. На основу оваквог дијаграма, датог за цело становништво, сазнали бисмо колико има људи са примањима "од 16.000 до 18.000" а колико нпр. "од 160.000 до 500.000". Користан дијаграм би био и онај који приказује расподелу доходака по тзв. перцентилима (термин објашњен такође на самом почетку курса, на стр. 3 књиге ). Шта би био нпр. 90-ти перцентил? То би био онај износ плате испод кога се налази 90 % свих плата запослених. Погледајмо Графикон 2: види се да нпр. 90-том перцентилу одговара износ дохотка од 80.000 динара, што значи да, у примеру предузећа из Табеле 1, деведесет одсто запослених прима мање од 80.000 динара. Осамдесети перцентил износи 24.000 динара, дакле 80 % запослених прима мање од тога. Објавивши овакав дијаграм, новинар обезбеђује тачнију интерпретацију стања у предузећу или целокупној економији, односно више није могуће некоме "продати" причу о сарми. Такође је очигледно да није реч о некој сложеној и тешко схватљивој математици, која се не може објаснити читаоцима, као и да није тачно да статистика не поседује инструменте репрезентовања података на начин који би сачувао и пренео релевантне информације. Иако можда на први поглед то није очигледно, циљ овог текста није директна критика на рачун закључака из чланка објављеног у "Данас"-у. Аутор овог текста не сумња у стручност наших статистичара, али сматра да се њихови резултати неадекватно репрезентују путем медија. Намера аутора није ни да доводи у питање или критикује Паретово правило [4] већ да подигне ниво свести читалаца о томе шта је заиста статистика и како се она често неправилно користи у циљу тумачења података везаних за стандард грађана. [3] ] C.E. Weatherburn, A First Course in Mathematical Statistics, London: Cambridge University Press, 1968.
[4] Ј.P. Friedman, Dictionary of Business Terms, New York: Barron's Educational Series, 2000. Познато још и као "Правило 80-20", говори о томе да је дистрибуција прихода природно таква да приближно 80 % прихода нације доспева у руке свега око 20 % популације.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Од истог аутора
Остали чланци у рубрици
- Спољни утицај у Србији - како је домаћа економија подељена странцима?
- Циљеви санкција САД НИС-у - удар на успешну панчевачку рафинерију, откуп и продаја фирме другом купцу и прекид чврсте енергетске везе Русије и Србије
- Одговор Рио Тинту - Наведите на шта сте потрошили 500 милиона долара за које тврдите да сте до сада већ уложили у пројекат „Јадар“
- Шта добија Србија од пројекта "Јадар"? Ризик велики, а добит мала и неизвесна
- Колико нас стварно коштају Вучићеви пројекти - актуелна власт скоро утростручила дуг са 2150 на 5750 евра по глави становника
- ЕУ отворено заинтересована за српски литијум - зашто еколошке студије наручује Рио Тинто, а не држава Србија
- Назире ли се крај "литијумске грознице"
- Електрични аутомобили - скупа и не баш толико „еколошка“ играчка
- Место Београда на новом „Путу свиле“ - кинеске компаније и инвестиције главни генератор садашњег српског индустријског раста
- Из архиве НСПМ - Србија и Европска унија (2015)

.jpg)







 Питање просечне плате, као репрезента стандарда грађана, стално се провлачи кроз медије и извор је бројних полемика и скепсе према статистици као науци. Овај чланак има за циљ да бар делимично разјасни најважније недоумице и покаже да статистика поседује инструменте репрезентовања података на начин који би сачувао и пренео релевантне информације, али је ово могуће само ако се то не чини тенденциозно.
Питање просечне плате, као репрезента стандарда грађана, стално се провлачи кроз медије и извор је бројних полемика и скепсе према статистици као науци. Овај чланак има за циљ да бар делимично разјасни најважније недоумице и покаже да статистика поседује инструменте репрезентовања података на начин који би сачувао и пренео релевантне информације, али је ово могуће само ако се то не чини тенденциозно.